高考真题
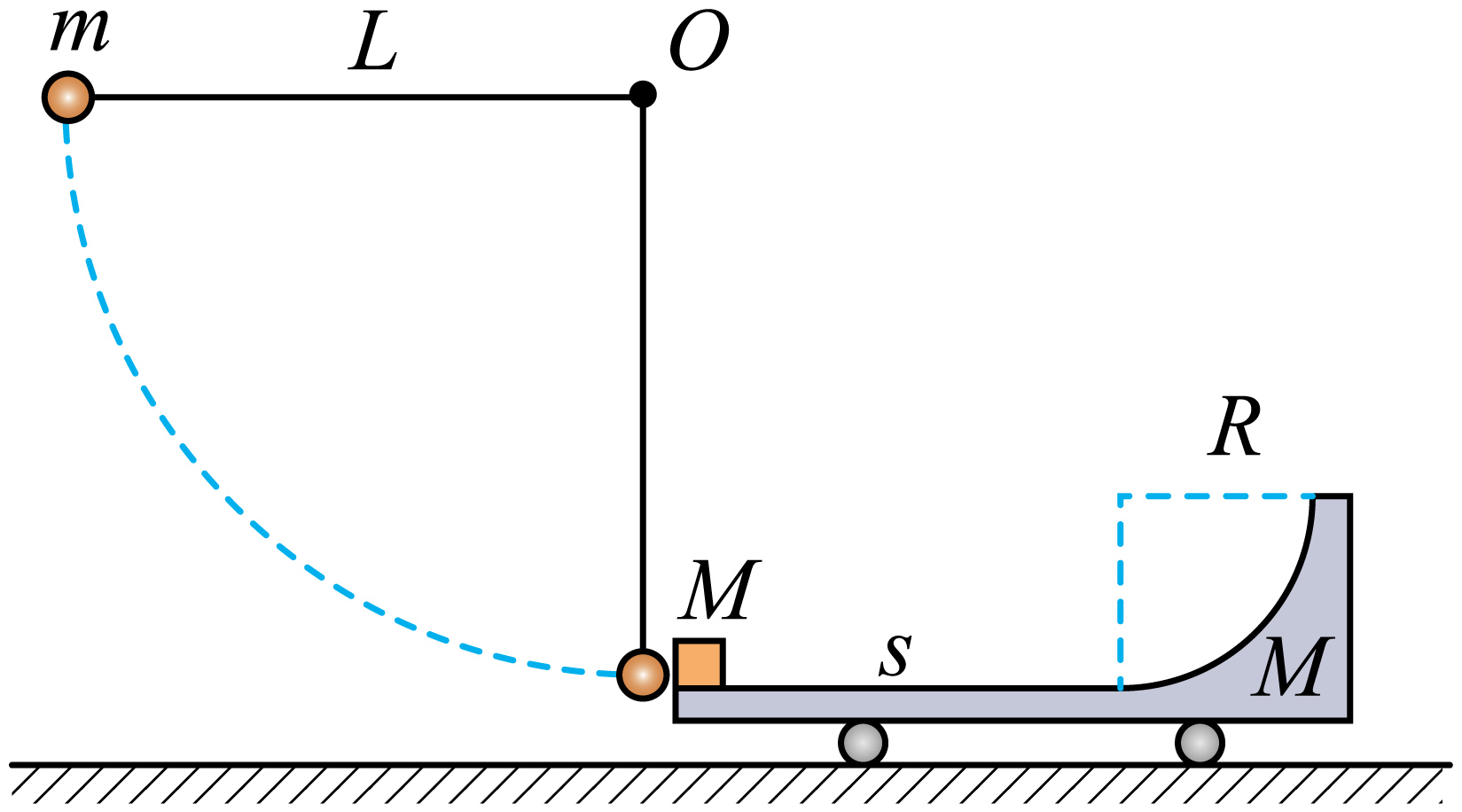
(2024安徽高考题14题)如图所示,一实验小车静止在光滑水平面上,其上表面有粗糙水平轨道与光滑四分之一圆弧轨道。圆弧轨道与水平轨道相切于圆弧轨道最低点,一物块静止于小车最左端,一小球用不可伸长的轻质细线悬挂于O点正下方,并轻靠在物块左侧。现将细线拉直到水平位置时,静止释放小球,小球运动到最低点时与物块发生弹性碰撞。碰撞后,物块沿着小车上的轨道运动,已知细线长L=1.25m。小球质量m=0.20kg。物块、小车质量均为M=0.30kg。小车上的水平轨道长s=1.0m。圆弧轨道半径R=0.15m。小球、物块均可视为质点。不计空气阻力,重力加速度g取10m/ s^2。
(1)求小球运动到最低点与物块碰撞前所受拉力的大小;
(2)求小球与物块碰撞后的瞬间,物块速度的大小;
(3)为使物块能进入圆弧轨道,且在上升阶段不脱离小车,求物块与水平轨道间的动摩擦因数\mu的取值范围。
解: (1)从释放到最低点过程由动能定理得: mgL=\frac{1}{2}mv^2-0
在最低点由牛二定律有:F_N-mg=\frac{mv^2}{L}
解得: F_N=3mg=6N
(2)弹性碰撞机械能守恒: \frac{1}{2}mv^2=\frac{1}{2}Mv_{球}^2+\frac{1}{2}Mv_{木}^2
球和木块动量守恒: mv=Mv_{球}+Mv_{木}
解得: v_{球}=-1m/s,v_{木}=4m/s
当然直接解会比较麻烦,结合弹性碰撞,碰撞系数为1更好解
v_{相对} = -v'_{相对}
v-0 = v_{木}-v_{球}
(3)只要木块没离开小车,木块和小车组成的系统水平方向没有外力干扰,因此水平方向动量守恒。
木块恰好运动到圆最低点达到共速,此时由动量守恒得:
Mv_{木块}=2Mv_3 \tag{3.1}
过程能量守恒得: \frac{1}{2}Mv^2_{木块}=2\cdot\frac{1}{2}Mv^2_3+uMgs\tag{3.2}
由(3.1),(3.2)得:
u_1=0.4
木块恰好能运动圆的最高点,此时竖直方向分速度为0,只有水平速度。此时由动量守恒得:
Mv_{木块}=2Mv_4 \tag{3.3}
\frac{1}{2}Mv^2_{木块}=2\cdot\frac{1}{2}Mv^2_3+uMgs+MgR\tag{3.4}
由(3.3),(3.4)得:
u_1=0.25
综上所述动摩擦因数取值范围:
0.25 \leq \mu<0.4
其实能量守恒也能写成质点系的动能定理,质点系动能变化包括所有外力做功还有内力做功之和。 其中支持力和压力不做功,因为木块和轨道不分离,沿着弹力方向这一对弹力做功之和为0。 摩擦力做功之和看相对位移。再还有重力对木块做功,因此(3.4)式可以这么理解:
系统动能变化:2\cdot\frac{1}{2}Mv^2_3-\frac{1}{2}Mv^2_{木块}
一对摩擦力做功: -uMgs
重力对木块做功: -MgR
综上: -uMgs-MgR=2\cdot\frac{1}{2}Mv^2_3-\frac{1}{2}Mv^2_{木块}