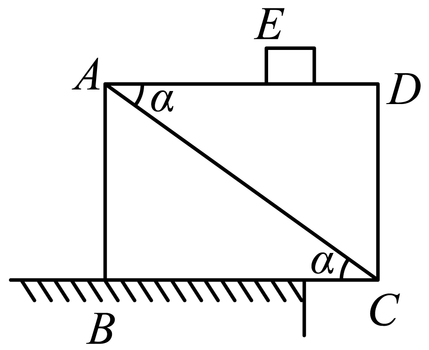
2.如图1所示.为斜面重合的两楔块ABC及ADC,质量均为M,AD、BC两面成水平,E为质量等于m的小滑块,楔块的倾角为α,各面均光滑,系统放在水平平台角上从静止开始释放,求两斜面未分离前E的加速度.
解法:
以地面为参考系,水平向右为x正方向,竖直向下为y正方向,E贴着楔块ADC下降,E只受重力和支持力,只有竖直y方向加速度记为a_{Ey}.
楔块ADC的加速度分解为水平向右x方向和水平向右y方向a_{2x}和a_{2y}
楔块ABC有水平向左的加速度a_{1x}
楔块ADC和ABC水平方向合力为0,水平方向动量守恒。因此
a_{1x}=a_{2x}
或者从其他角度分析,
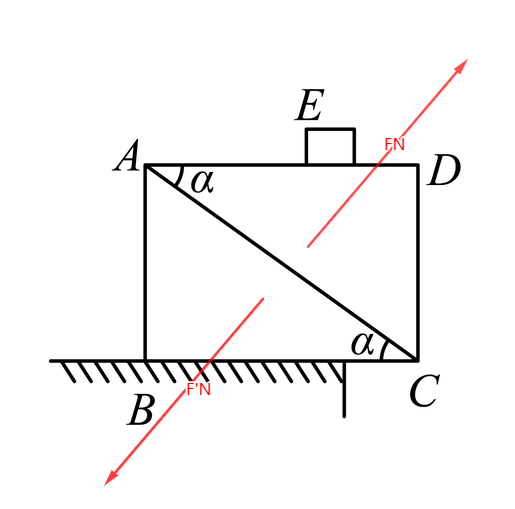
两楔块ADC和ABC之间的弹力FN大小相等方向相反,各自在水平方向贡献了分力,水平方向不受其他力。因此
a_{1x}=a_{2x} ~~~~(1)
滑块E贴着楔块ADC往下移动,因此
a_{Ey}=a_{2y}~~~~(2)
对滑块E受力分析,列牛二定律:
mg-F_{N1}=ma_{Ey}~~~~(3)
对楔块ADC受力分析,列牛二定律: 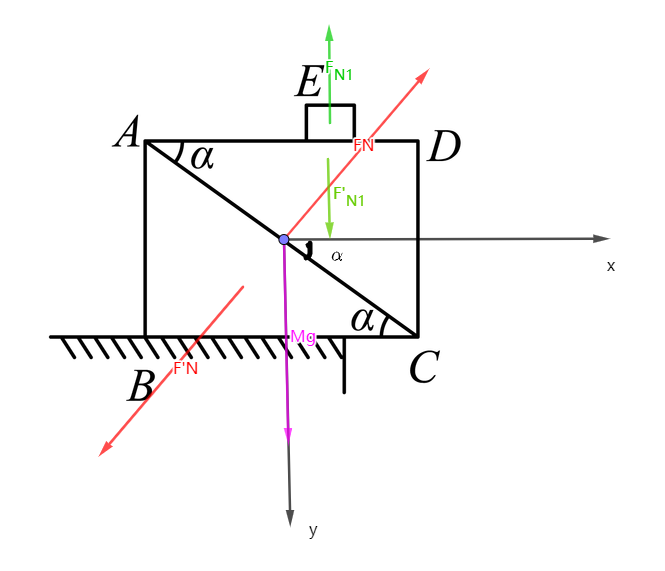
x方向:F_{N}~sin\alpha = M~a_{2x}~~~~(4)
y方向: F_{N1}+Mg-F_N~cos\alpha=M~a_{2y} ~~~~(5)
以楔块ABC为参考系,楔块ADC沿着AC面加速下滑,因此加速度满足如下关系:
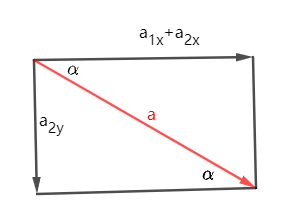
\frac{a_{2y}}{2a_{2x}} = tan\alpha ~~~~(6)
联立(1)-(6)方程解得: a_{Ey}=\frac{(M+m)g}{m+M+\frac{M}{2tan^2\alpha}}=\frac{2(M+m)~g~sin^2\alpha}{2(m+M)sin^2\alpha+Mcos^2\alpha}
Note that there are five types of callouts, including: note, warning, important, tip, and caution.
This is an example of a callout with a title.
This is an example of a ‘folded’ caution callout that can be expanded by the user. You can use collapse="true" to collapse it by default or collapse="false" to make a collapsible callout that is expanded by default.