基本公式法:
经典例题
- 一辆汽车在笔直的公路上做匀变速直线运动,该公路安置三个路标A、B、C。A、B 间距s_{1}=6m, B、C间距s_{2}=24m。汽车通过A、B两相邻路标用了t_{1}=2s, 通过B、C两相邻路标用了t_{2}=4s。求:
(1)汽车通过A、C路标间距的平均速度大小;
(2)汽车的加速度大小及汽车通过A、B、C各路标时的速度大小。
 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩
① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩
解法一:基本式
A\rightarrow B:s_1=v_At_1+\frac{1}{2}at_1^2 \quad
A\rightarrow C:s_1+s_2=v_A(t_1+t_2)+\frac{1}{2}a(t_1+t_2)^2\quad
联立①②方程组,解得:v_A=2m/s,a=1m/s^2
v_B=v_A+at_1=4m/s,v_c=v_A+a(t_1+t_2)=8m/s
解法二:平均速度=中间时刻速度
v_{1s末}=\bar{v}_{AB}=3m/s
v_{4s末}=\bar{v}_{BC}=6m/s
a=\frac{\Delta v}{\Delta t}=1m/s^2
v_A=v_{1s末}-a\frac{t_1}{2}=2m/s
解法三:位移差公式
BC段分为等时的两段BP,PC,则由位移差公式可得 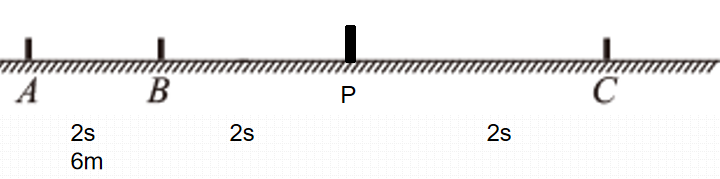
x_{BP}-s_1=x_{PC}-x_{BP}
x_{BP}+x_{PC}=s_2
解得x_{BP}=10m,x_{PC}=14m \Delta x=x_{BP}-x_{AB}=at_1^2
解得 a=1m/s^2
变式1:
3.如图,一质点从 A点开始做初速度为零 的匀加速直线运动,加速度大小为 a , B 、 C 、 D 是质点运动路径上的三个点, 且 BC=x_1 , CD=x_2 ,质点通过BC 段所用时间是通过CD 段所用时间的一半, 则质点经过C 点时的速度大小和 A 、 B 间的距离为( )

A.质点经过 C 点时的速度大小为 \frac{x_1+4x_2}6\sqrt{\frac{3a}{x_2-2x_1}}
B.质点经过 C 点时的速度大小为\frac{4x_1+x_2}6\sqrt{\frac{3a}{x_2-2x_1}}
C. A 、 B 间的距离为 \frac{(8x_{1}-x_{2})^{2}}{24(x_{2}-2x_{1})}
D. A 、 B 间的距离为 \frac{(8x_{1}-x_{2})^{2}}{12(x_{2}-2x_{1})}
解:设BC段时间为t,则CD段时间为2t。
B-C:v_Bt_0+\frac{1}{2}at_0^2=x_1 \quad(1)
B-D:v_B\cdot 3t_0+\frac{1}{2}a(3t_0)^2=x_1+x_2\quad(2)
(2)-3*(1)\rightarrow at_0^2=\frac{x_2-2x_1}{3}\quad(3)
9*(1)-(2)\rightarrow v_Bt=\frac{8x_1-x_2}{6}\quad(4)
t_0=\sqrt{\frac{x_2-2x_1}{3a}}
v_B=\frac{8x_1-x_2}{6t_0}=\frac{8x_1-x_2}{6}\sqrt{\frac{3a}{x_2-2x_1}}
x_{AB}=\frac{v_B^2}{2a}=\frac{(8x_{1}-x_{2})^{2}}{24(x_{2}-2x_{1})}
由(3)得:at_0=\frac{x_2-2x_1}{3t_0}=\frac{x_2-2x_1}{3}\sqrt{\frac{3a}{x_2-2x_1}}
v_C=v_B+at_0=\frac{4x_1+x_2}{6}\sqrt{\frac{3a}{x_2-2x_1}}
故选BC
变式2:
3.已知0、A、B、C为同一直线的四点,AB间的距离为l_1,BC间的距离为l_2,一物体自0点由静止出发,沿此直线做匀加速运动,依次经过A、B、C三点,已知物体通过AB段与BC段所用的时间相等。求O与A的距离。

解:设A到B时间为T,加速度为a,A点速度为 v_A
A到B:l_1=v_AT+\frac{1}{2}aT^2 \quad(1)
A到C:l_1+l_2=v_A\cdot 2T+\frac{1}{2}a\cdot(2T)^2\quad(2)
(1)(2)两个方程,三个未知量无法求解,但是可以找出三个未知量之间的关系。做如下处理:
(2)-2*(1),得到l_2-l_1=aT^2① \quad 即位移差公式
4*(1)-(2),得到2v_AT=3l_1-l_2 ②\quad
x_{OA}=\frac{v_A^2}{2a}=\frac{(3l_1-l_2)^2}{4T^2}\cdot\frac{1}{2a}=\frac{(3l_1-l_2)^2}{8(l_2-l_1)}
逆向思维
2.疫情期间,武汉小汤山医院7天内建成,见证了中国速度。在建筑工地上一卡车以速度10m/s匀速行驶,刹车后第1个2s内的位移与最后一个2s内的位移之比为3∶2,设卡车做匀减速直线运动,则刹车后4s内卡车通过的距离是( )
A.2.5m
B.4m
C.12.5m
D.25m
解:
第一个2s内位移3s=v_0*2-\frac{1}{2}a\cdot2^2
最后一个2s内位移,逆向思维,看成初速度为0的反向加速运动: 2s=\frac{1}{2}a\cdot2^2
解得 s=4m,a=4m/s^2
v_0=10m/s,t=2.5s停下,因此4s内位移:x=\frac{v_0^2}{2a}=12.5m
注意逆向思维:匀减速至0的运动可以看成反向的初速度为0的匀加速运动解决问题
一题多解
1.目前交警部门开展的“车让人”活动深入人心.司机发现前方有行人正通过人行横道时开始做匀减速直线运动,恰好在停车线处停止运动.汽车经 4 s停止,若在第 1 s 内的位移是14 m ,则最后 1 s内的位移大小是( )
A. 3.5 m B. 2 m C. 1 m D. 0 m
解法一基本公式:
第1秒内位移14m:v_0\cdot1-\frac{1}{2}a\cdot 1^2=14\quad(1)
4s减速为0:v_0-4a=0\quad(2)
联立(1)(2)方程组解得:
v_0=16m/s
a=4m/s^2
最后一秒内位移s=\frac{1}{2}at^2=\frac{1}{2}a\cdot 1=2m
解法二:中间时刻速度等于平均速度
v_{0.5s末}=\bar{v}_{第1s内}=14m/s
v_{4s末}=0m/s
a=\frac{\Delta v}{\Delta t}=-4m/s^2
\bar{v}_{最后一秒内}=v_{3.5s末}=v_{0.5s末}-a\cdot 3=2m/s^2
最后一秒内位移:x=\bar{v}_{最后1s内}\cdot 1s=2m
解法三:比例关系、逆向思维
减速运动可以看成反向的初速度为0的匀加速运动,因此满足以下比例关系:
x_{第1s内}:x_{第2s内}:x_{第3s内}:x_{第4s内}=7:5:3:1
x_{第1s内}=14m
x_{第4s内}=2m
2.一物体做匀加速直线运动,初速度v_0=2m/s^2,他在第3s内通过的位移是4.5m,则它的加速度为( )
A.0.5m/s^2
B.1m/s^2
C.1.5m/s^2
D.2.0m/s^2 **** 3.一物体做匀加速直线运动,通过一段位移\Delta x所用时间为t_1,紧接着通过下一段位移\Delta x所用时间为t_2。则物体的加速度为( )
A.\frac{2\Delta x (t_1-t_2)}{t_1t_2(t_1+t_2)}
B.\frac{\Delta x (t_1-t_2)}{t_1t_2(t_1+t_2)}
C.\frac{2\Delta x (t_1+t_2)}{t_1t_2(t_1-t_2)}
D.\frac{\Delta x (t_1+t_2)}{t_1t_2(t_1-t_2)}